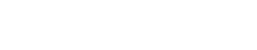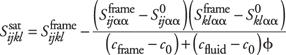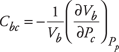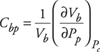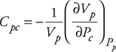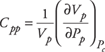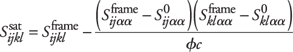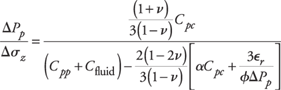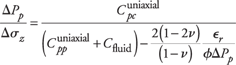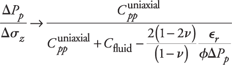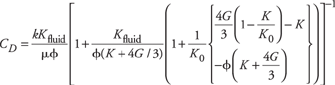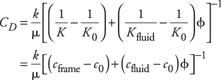Geophysics/ 4D
Can tidal-driven pressure changes reveal reservoir properties for use in 4D monitoring?
As the tides change, the overburden pressure changes. This can be seen in reservoir-emplaced pressure gauges. These measurements can provide in situ information about rock properties that laboratory core measurements might not.
Dirk Smit, Shell, and Colin M. Sayers, Schlumberger
Time-lapse seismic can be used to monitor changes in fluid saturation and pressure due to production. Interpreting such measurements, however, requires knowing how the in situ pore-volume compressibility and fluid bulk modulus vary with changes in saturation and pressure. Reservoir pressure measurements often show changes due to tidal effects. These variations can be analyzed to obtain constraints on the pore-volume compressibility and fluid bulk modulus. With the increasing use of highly accurate and sensitive downhole pressure gauges, measurements of tidal-induced variations combined with time-lapse seismic data promise to lead to significant improvements in reservoir monitoring.
This article is written for both mathematical and non-mathematical discussion. However, this topic has seen considerable advances in mathematical modeling of reservoir attributes over the past 15 years or so. Corrections and discussions of common misconceptions and errors are given. Application to a North Sea data set is also discussed.
INTRODUCTION
Early evidence for variations in aquifer pressure due to ocean tides comes from measurements of water levels in wells.1 As early as 77 A.D., Pliny the Elder reported variations in water level in a well near the temple of Hercules in Cadiz related to ocean tides.1,2 In 1902, the United States Geological Survey reported water-level variations in wells in Atlantic City, New Jersey that varied with ocean depth.1,3
But even in deep oil wells, tides can change reservoir pressure, as shown in Fig. 1. These variations have been observed in several North Sea oilfields.4
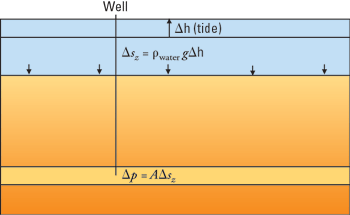 |
Fig. 1. Changes in water column height due to tides result in changes in reservoir pressure.
|
|
In 4D seismic studies, the difference between two or more seismic data sets, acquired at different times during production, is used to infer changes in saturation and reservoir pressure. Such data hopefully show that the reservoir is sensitive to changes due to production, sufficient to show a 4D difference. Two fundamental reservoir properties that reveal these changes are fluid bulk modulus and reservoir compressibility.
While the porosity, fluid bulk modulus and moduli of the drained, porous frame can be measured in a laboratory on cores, uncertainties exist due to possible damage in the cores, the uncertainty in the fluid bulk modulus due to unknown fluid distribution (e.g., patchy vs. homogeneous), and the fact that core plugs are an extremely small sample of reservoir volume. Clearly, interpreting 4D seismic would be greatly aided if independent constraints on these parameters could be obtained. The authors propose using tidal measurements for this purpose.
ROCK COMPRESSIBILITY COEFFICIENTS
Changes in bulk volume and pore volume may occur due to changes in the confining pressure and/or pore pressure. These two types of volume, combined with the two types of potential pressure changes, results in four rock compressibilities. These are defined by Zimmerman5 and are:
- Cbc, the variation in bulk volume with change in confining stress at constant pore pressure and, therefore, represents the compressibility of the frame
- Cbp, the variation in bulk volume with change in pore pressure at constant confining stress, which, therefore, describes subsidence
- Cpc, the variation in pore volume with change in confining stress at constant pore pressure
- Cpp, describes the variation in pore volume with change in pore pressure at constant confining stress and is the pore volume compressibility.
Given C 0 as the compressibility of the rock matrix material, and assuming the mineral grains to be microscopically homogeneous, Zimmerman5 shows the four rock compressibility coefficients are related by:
It follows that a measurement of one of the rock compressibilities provides a constraint on the others. See shaded sidebar for an example of this constraint.
| |
Rock compressibility |
|
| |
For the case of a reservoir of porosity f with an anisotropic frame with compliance tensor 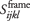 , the compliance tensor of the rock, , the compliance tensor of the rock, 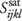 , containing a fluid with compressibility cfluid is given by Brown and Korringa:6 , containing a fluid with compressibility cfluid is given by Brown and Korringa:6
| |
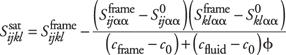 |
(4) |
where c frame is the compressibility of the frame.
Consider a porous rock with bulk volume Vb and pore volume Vp. Changes in Vb and Vp may occur due to changes in the confining pressure, Pc, and pore pressure, Pp, and may be written in terms of the four rock compressibilities Cbc, Cbp, Cpc and Cpp defined by Zimmerman5 and previously described:
|
|
| |
Well testing example |
|
| |
Consider the relation between well testing, which involves the pore volume compressibility Cpp and time-lapse seismic, which involves the frame compressibility Cbc. In radial coordinates, the diffusion equation relating the variation in pressure, p, with time, t, is
| |
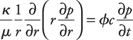 |
(9) |
where 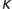 is the permeability, µ is the fluid viscosity, f is the total connected porosity and c is the total compressibility of the pore/ fluid system (see also, The Diffusion Equation, below). c can be written in terms of the fluid compressibility cfluid and the pore space compressibility cpp as is the permeability, µ is the fluid viscosity, f is the total connected porosity and c is the total compressibility of the pore/ fluid system (see also, The Diffusion Equation, below). c can be written in terms of the fluid compressibility cfluid and the pore space compressibility cpp as
| |
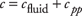 |
(10) |
Now, 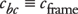 . So, recalling Zimmerman’s rock compressibility coefficients relations for cpp and cbc in Eqs. 1, 2 and 3, the storage capacity of the rock, fc, may be written in the form . So, recalling Zimmerman’s rock compressibility coefficients relations for cpp and cbc in Eqs. 1, 2 and 3, the storage capacity of the rock, fc, may be written in the form
| |
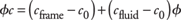 |
(11) |
which is exactly the denominator in equation (4), as pointed out by Cardona.7 Hence,
| |
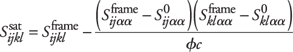 |
(12) |
where fc may be constrained using well test information.
|
|
| |
Reservoir pressure changes caused by tides |
|
| |
For simplicity, consider the case of an isotropic reservoir. The equations of poroelasticity are then:
where 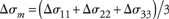
Defining 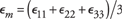 , it follows that , it follows that
where
| |
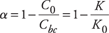 |
(19) |
Hence,
| |
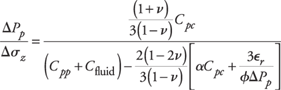 |
(20) |
It should be noted that equation (20) is valid for any Biot constant, and therefore can be applied for both loading and unloading as shown in Fig. 3.
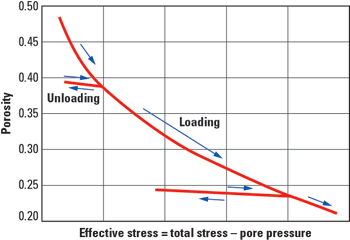 |
Fig. 3. 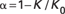 may be significantly less than 1 for unloading (e.g., water injection). may be significantly less than 1 for unloading (e.g., water injection).
|
|
Now from Zimmerman,8
| |
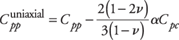 |
(21) |
|
|
|
|
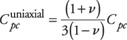 |
(22) |
Hence,
| |
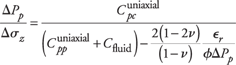 |
(23) |
In the limit of incompressible grains
Hence,
| |
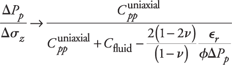 |
(24) |
Assuming zero lateral strain, Îr = 0,
| |
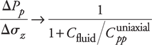 |
(25) |
|
|
|
NORTH SEA EXAMPLE
Fig. 2 (middle) shows an example of a tidal measurement from the North Sea. The tide predicted for this location is shown in Fig. 2 (top), and a comparison of the predicted variation in reservoir pressure with the measured reservoir pressure is shown in Fig. 2 (bottom). The agreement is seen to be excellent. The time delay between the tide and the measured pressure has been removed in this example. Application of the theory then allows the pore volume compressibility of the rock to be determined.
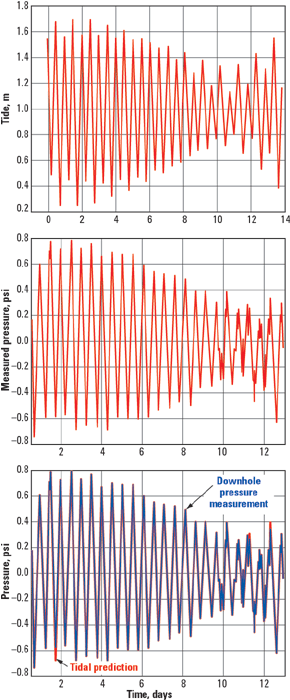 |
Fig. 2. An example of a tidal measurement from the North Sea. Top, tide predicted for the location of the North Sea example. Center, measured reservoir pressure variations. Bottom, comparison of measured vs. predicted pressure response.
|
|
CONCLUSION
Although time-lapse seismic measurements have been used widely to monitor changes in saturation and pressure due to production, reliable estimates of the change in saturation and fluid pressure in the reservoir require knowledge of the variation in pore volume compressibility and fluid bulk modulus with fluid saturation and reservoir pressure. These variations can be studied in the laboratory, but uncertainties exist.
Rock compressibilities governing time-lapse seismic, subsidence, tidal effects and well tests are all related and can provide important constraints on each other. A theory of the tidal effect has been derived that is valid for transversely isotropic sediments and any value of Biot’s constant.
Changes in sea level due to tides cause variations in reservoir pressure that can be measured using downhole pressure sensors. These variations can be analyzed to obtain constraints on the pore volume compressibility and fluid bulk modulus, and therefore provide important constraints for the interpretation of time-lapse seismic measurements.
It is expected that increasing use of permanent downhole pressure sensors will allow more routine measurement of changes in reservoir pressure due to tidal effects. These will be used in combination with time-lapse seismic measurements to monitor changes in saturation and pressure resulting from production. 
ACKNOWLEDGMENT
We thank Niek van den Beukel (Shell) for useful discussions and for providing the data shown in Fig. 2.
LITERATURE CITED
1 Wang, H. F., “Theory of linear poroelasticity,” Princeton University Press, Princeton, 2000.
2 Melchior, P. J., “The tides of the planet Earth,” Pergamon, New York, 1983.
3 Meinzer, O. E., “Compressibility and elasticity of artesian aquifers,” Econ. Geol. Vol. 23, pp. 263-291, 1928.
4 Dean, G. A., Hardy, R., and P. Eltvik, “A new method to monitor compaction and compressibility changes in offshore chalk reservoirs by measuring formation pressure variations caused by the sea tide,” SPE 23142, Offshore Europe Conference, Aberdeen, 3-6 September, 1991.
5 Zimmerman, R. W., “Compressibility of sandstones,” Elsevier, Amsterdam, 1991.
6 Brown, R. J. S. and J. Korringa, “On the dependence of the elastic properties of porous rock on the compressibility of the pore fluid,” Geophysics, Vol. 40, pp. 608-616, 1975.
7 Cardona, R., Ozkan, E., and M. Batzle, “Integrating pressure-transient and seismic data to determine the characteristics of single- and double-porosity reservoirs,” SPE 77451, 2002 SPE Annual Technical Conference and Exhibition.
8 Zimmerman, R.W., “Implications of static poroelasticity for reservoir compaction,” in Proc. 4th North Amer. Rock Mech. Symp., A. A. Balkema, Rotterdam, pp. 169-72, 2000.
9 Biot, M. A., “General theory of three-dimensional consolidation,” J. Appl. Phys. Vol. 12, pp. 155-164, 1941.
10 Biot, M.A., “Theory of propagation of elastic waves in a fluid-saturated porous solids: I. Low-frequency range,” J. Acoust. Soc. Am., Vol. 28, pp. 168-178, 1956.
11 Biot, M. A., “Theory of propagation of elastic waves in a fluid-saturated porous solids: II. Higher frequency range,” J. Acoust. Soc. Am. Vol. 28, pp. 179-191, 1956.
12 Biot, M. A. and D. G. Willis, “The elastic coefficients of the theory of consolidation,” J. Appl. Phys. Vol. 24, pp. 594-601, 1957.
13 Biot, M.A., “Mechanics of deformation and acoustic propagation in porous media,” J. Appl. Phys. Vol. 33, pp. 1482-1498, 1962.
14 Rice, J. R. and M. P. Cleary, “Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents,” Rev. Geophys. Space Phys. Vol. 14, pp. 227-241, 1976.
15 Chandler, R. N. and Johnson, “The equivalence of quasistatic flow in fluid-saturated porous media and Biot’s slow wave in the limit of zero frequency,” J. Appl. Phys. Vol. 52, pp. 3391-3395, 1981.
16 Dake, L. P., “Fundamentals of reservoir engineering,” Elsevier,1978.
17 Culham, W. E., SPE Journal Vol. 14, pp. 545, 1974.
| |
The Diffusion Equation |
|
| |
The diffusion equation describing quasistatic flow in fluid-saturated porous media can be derived from the theory formulated by Biot.9–13 This is the theory of elastic and viscous behavior of macroscopically homogeneous, isotropically porous elastic media, saturated with a compressible viscous fluid. Rice and Cleary14 show that the fluid mass content m per unit volume satisfies a homogeneous diffusion equation:
| |
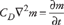 |
(A1) |
where CD is the diffusion constant. Expressing the drained and undrained Poisson’s ratios in the expression for CD given by Rice and Cleary in terms of the bulk modulus of the fluid, Kfluid, the bulk and shear modulus of the rock frame, K and G, and the bulk modulus of the rock matrix material, K0, Chandler and Johnson15 show that CD takes the form:
| |
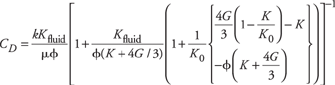 |
(A2) |
Here, k is the permeability and f the porosity of the rock, and µ is the viscosity of the fluid.
For the case of a borehole in an infinite domain, subject to axisymmetric loading, Rice and Cleary show that equation (A1) leads to a homogeneous diffusion equation for the fluid pressure, p:
| |
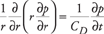 |
(A3) |
It is interesting to consider two limits:
1. If the shear modulus of the frame is equated to zero, it follows from equation (A2) that
| |
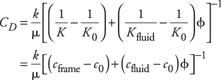 |
(A4) |
which is in agreement with equations (9) and (11). Although these equations appear to be widely used in reservoir engineering (e.g., Dake16), the shear modulus of the frame is usually of the same order as the frame bulk modulus in most rocks and cannot be neglected.
2. In the limit K, G >>Kfluid, equation (A2) reduces to
| |
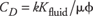 |
(A5) |
This equation has been used quite extensively in well-to-well pressure-pulse testing in the oil industry.15, 17
Fig. 4 compares the diffusivity given by equations (A4) and (A5) with the exact equation (A2) as a function of K /K0 for various values of Poisson’s ratio, n, of the frame given by
It is assumed that the porosity f = 0.3, the permeability k = 0.1 Darcy, the bulk modulus of the solid grains K0=37 GPa, and that the pore fluid is water with viscosity and bulk modulus Kfluid=2.2 GPa.
It is seen in Fig. 4 that equation (A5) substantially overestimates the diffusivity, CD, while equation (A4) underestimates CD, particularly for small values of Poisson’s ratio typical of sands.
Chandler and Johnson15 show that the diffusivity given by equation (A2) is identical to the diffusivity of the Biot slow wave.10 In Biot theory the motion of the solid and fluid constituents are treated on an equal footing. This theory therefore represents the most general effective medium theory possible for two-component solid/ fluid systems.15
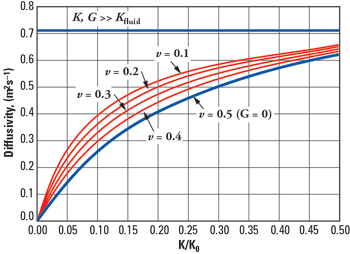 |
Fig. 4. Diffusivity, CD, predicted by equations (A2), (A4) and (A5) as a function of K/K0 for various values of Poisson’s ratio of the frame, n.
|
|
|
|
|
THE AUTHORS
|
 |
Dirk Smit earned an undergraduate degree in 1985 in theoretical physics and mathematics from the Univ. of Amsterdam, and a PhD in 1989 from the Inst. for Theoretical Physics, Univ. of Utrecht. Work experience includes the Theoretical Physics Dept. at the Univ. of California – Berkeley until end 1991, then on to Shell, where he started in EP Research. Together with co-workers he introduced modern mathematical physics methods to establish imaging conditions for Kirchhoff seismic imaging in the presence of acoustic caustics, for which he received Shell’s Gold Award for Best R&D (1994). After assignments in the UK, where he was Chief Geophysics for Shell Expro and responsible for Shell’s 4D reservoir monitoring program in the North Sea, he is currently manager of Exploration Technology, Shell International Exploration and Production in the Netherlands. He won the Ludwig Mintrop Award (EAGE, 2001), is a member of SEG and EAGE and holds a visiting Professorship in Geophysics at the School of Earth Sciences at Leeds Univ. in the UK.
|
|
|
 |
Colin M. Sayers is a Scientific Advisor in the Schlumberger Data & Consulting Services Geomechanics Group in Houston, providing consultancy in pore pressure prediction, wellbore stability analysis, geomechanics, rock physics, geophysics and the properties of fractured reservoirs. His technical expertise includes pore pressure, fracture gradient and drilling hazard prediction, analysis of production-induced reservoir stress changes, subsidence, fault reactivation, 3D mechanical earth modeling, fractured reservoir evaluation, borehole/ seismic integration, stress-dependent acoustics, rock mechanics and fluid flow in fractured reservoirs. He has received the Conrad Schlumberger Award for “Outstanding Paper for Technical Depth” for the paper “Prediction of reservoir pore pressure, compaction, casing deformation and surface subsidence using a 3D Mechanical Earth Model” presented at the Schlumberger Reservoir Symposium 2004. He earned a BA in physics in 1973 while at the Univ. of Lancaster, then a DIC in mathematics/ physics in 1977, and a PhD in theoretical solid state physics 1977, from Imperial College. He is a member of the SPE, SEG, EAGE, ARMA and AGU and is a member of the Research Committee of the SEG. He has published more than 100 technical papers.
|
| |
|
|